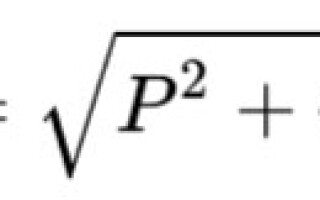เราทุกคนเจอเครื่องใช้ไฟฟ้าทุกวันดูเหมือนว่าชีวิตเราจะหยุดโดยไม่มีพวกเขา และแต่ละอันในคำแนะนำทางเทคนิคบ่งบอกถึงพลัง วันนี้เราจะหาว่ามันคืออะไรเรียนรู้ประเภทและวิธีการคำนวณ
เนื้อหา
กำลังไฟฟ้าในวงจรไฟฟ้ากระแสสลับ
เครื่องใช้ไฟฟ้าที่เชื่อมต่อกับแหล่งจ่ายไฟหลักทำงานในวงจรไฟฟ้ากระแสสลับ ดังนั้นเราจะพิจารณากำลังไฟฟ้าในสภาวะเหล่านี้ อย่างไรก็ตาม ก่อนอื่น ให้คำจำกัดความทั่วไปของแนวคิดก่อน
พลัง - ปริมาณทางกายภาพที่สะท้อนถึงอัตราการแปลงหรือการส่งพลังงานไฟฟ้า
ในความหมายที่แคบกว่านั้น พวกเขากล่าวว่ากำลังไฟฟ้าคืออัตราส่วนของงานที่ทำในช่วงระยะเวลาหนึ่งต่อช่วงเวลานี้
ในการถอดความคำจำกัดความนี้ในเชิงวิทยาศาสตร์น้อยลง ปรากฎว่าพลังงานคือพลังงานจำนวนหนึ่งที่ผู้บริโภคใช้ไปในช่วงระยะเวลาหนึ่ง ตัวอย่างที่ง่ายที่สุดคือหลอดไส้ธรรมดา อัตราที่หลอดไฟแปลงไฟฟ้าที่ใช้เป็นความร้อนและแสงคือพลังงาน ดังนั้น ยิ่งตัวบ่งชี้นี้สูงสำหรับหลอดไฟในขั้นต้น ยิ่งใช้พลังงานมาก และให้แสงสว่างมากขึ้น
เนื่องจากในกรณีนี้ไม่ได้มีเพียงกระบวนการแปลงไฟฟ้าเป็นอย่างอื่นเท่านั้น (แสง ความร้อน ฯลฯ) แต่ยังรวมถึงกระบวนการสั่นของสนามไฟฟ้าและสนามแม่เหล็กด้วย การเลื่อนเฟสจะปรากฏขึ้นระหว่างกระแสและแรงดันไฟ และสิ่งนี้ควรนำมาพิจารณาในการคำนวณเพิ่มเติม
เมื่อคำนวณกำลังไฟฟ้าในวงจรไฟฟ้ากระแสสลับ เป็นเรื่องปกติที่จะแยกแยะส่วนประกอบที่ทำงานอยู่ ปฏิกิริยาตอบสนอง และส่วนประกอบทั้งหมด
แนวคิดของพลังแอคทีฟ
พลังงานที่ "มีประโยชน์" ที่ใช้งานอยู่คือส่วนหนึ่งของพลังงานที่กำหนดลักษณะเฉพาะของกระบวนการแปลงพลังงานไฟฟ้าเป็นพลังงานอื่นโดยตรง เขียนแทนด้วยอักษรละติน P และวัดเป็น วัตต์ (อ.).
คำนวณตามสูตร: P = U⋅I⋅cosφ,
โดยที่ U และ I คือค่า rms ของแรงดันและกระแสของวงจร ตามลำดับ cos φ คือโคไซน์ของมุมเฟสระหว่างแรงดันและกระแส
สำคัญ! สูตรที่อธิบายข้างต้นนี้เหมาะสำหรับการคำนวณวงจรด้วย แรงดันไฟฟ้า 220Vอย่างไรก็ตาม หน่วยที่ทรงพลังมักใช้เครือข่ายที่มีแรงดันไฟฟ้า 380V ในกรณีนี้ นิพจน์ควรคูณด้วยรากของสามหรือ 1.73
แนวคิดของพลังงานปฏิกิริยา
พลังงาน "อันตราย" ที่เกิดปฏิกิริยาคือพลังงานที่เกิดขึ้นระหว่างการทำงานของเครื่องใช้ไฟฟ้าที่มีโหลดแบบเหนี่ยวนำหรือประจุไฟฟ้า และสะท้อนการสั่นของคลื่นแม่เหล็กไฟฟ้าที่กำลังดำเนินอยู่ พูดง่ายๆ ก็คือ นี่คือพลังงานที่ส่งผ่านจากแหล่งพลังงานไปยังผู้บริโภค แล้วกลับสู่เครือข่าย
แน่นอนว่ามันเป็นไปไม่ได้ที่จะใช้ส่วนประกอบนี้ในธุรกิจ ยิ่งไปกว่านั้น มันทำร้ายเครือข่ายแหล่งจ่ายไฟในหลาย ๆ ด้าน ดังนั้นพวกเขามักจะพยายามชดเชยมัน
ค่านี้แสดงด้วยตัวอักษรละติน Q
จดจำ! พลังงานปฏิกิริยาไม่ได้วัดเป็นวัตต์ทั่วไป (อ.) และในปฏิกิริยาโวลต์-แอมแปร์ (วาร์).
คำนวณตามสูตร:
Q = U⋅I⋅sin,
โดยที่ U และ I คือค่า rms ของแรงดันและกระแสของวงจร ตามลำดับ sinφ คือไซน์ของมุมเฟสระหว่างแรงดันและกระแส
สำคัญ! เมื่อคำนวณ ค่านี้สามารถเป็นได้ทั้งค่าบวกและค่าลบ ขึ้นอยู่กับการเคลื่อนที่ของเฟส
โหลดแบบคาปาซิทีฟและอุปนัย
ความแตกต่างที่สำคัญระหว่างปฏิกิริยา (capacitive และอุปนัย) โหลด - การมีอยู่ในความเป็นจริงของความจุและการเหนี่ยวนำซึ่งมักจะเก็บพลังงานและมอบให้กับเครือข่ายในภายหลัง
โหลดอุปนัยแปลงพลังงานของกระแสไฟฟ้าก่อนเป็นสนามแม่เหล็ก (ในช่วงครึ่งรอบครึ่ง) แล้วแปลงพลังงานของสนามแม่เหล็กเป็นกระแสไฟฟ้าและส่งไปยังเครือข่าย ตัวอย่าง ได้แก่ มอเตอร์เหนี่ยวนำ วงจรเรียงกระแส หม้อแปลงไฟฟ้า แม่เหล็กไฟฟ้า
สำคัญ! เมื่อใช้งานโหลดอุปนัย เส้นโค้งปัจจุบันจะล่าช้าโค้งแรงดันไฟฟ้าครึ่งรอบเสมอ
โหลด capacitive แปลงพลังงานของกระแสไฟฟ้าเป็นสนามไฟฟ้าแล้วแปลงพลังงานของสนามผลลัพธ์กลับเป็นกระแสไฟฟ้าทั้งสองกระบวนการดำเนินการอีกครั้งครึ่งรอบในแต่ละครั้ง ตัวอย่าง ได้แก่ ตัวเก็บประจุ, แบตเตอรี่, มอเตอร์ซิงโครนัส
สำคัญ! ในระหว่างการดำเนินการโหลดแบบ capacitive เส้นโค้งปัจจุบันจะนำเส้นโค้งแรงดันไฟฟ้าไปครึ่งรอบ
ตัวประกอบกำลัง cosφ
ตัวประกอบกำลังcosφ (อ่าน โคไซน์ phi) เป็นปริมาณสเกลาร์ทางกายภาพที่สะท้อนถึงประสิทธิภาพการใช้พลังงานไฟฟ้า พูดง่ายๆ ก็คือ ค่าสัมประสิทธิ์ cosφ แสดงถึงการมีอยู่ของส่วนปฏิกิริยาและค่าของส่วนแอคทีฟที่ได้รับสัมพันธ์กับกำลังทั้งหมด
ค่าสัมประสิทธิ์ cosφ หาได้จากอัตราส่วนของพลังงานไฟฟ้าที่ใช้งานต่อพลังงานไฟฟ้าที่ปรากฎ
บันทึก! ในการคำนวณที่แม่นยำยิ่งขึ้น ควรคำนึงถึงการบิดเบือนที่ไม่เป็นเชิงเส้นของไซนูซอยด์ด้วย อย่างไรก็ตาม การคำนวณแบบปกติจะละเลยสิ่งเหล่านี้ไป
ค่าของสัมประสิทธิ์นี้สามารถเปลี่ยนแปลงได้ตั้งแต่ 0 ถึง 1 (หากการคำนวณดำเนินการเป็นเปอร์เซ็นต์จากนั้นจาก 0% ถึง 100%). จากสูตรการคำนวณนั้นไม่ยากที่จะเข้าใจว่ายิ่งมีค่ามากเท่าไหร่ส่วนประกอบที่ใช้งานก็จะยิ่งมากขึ้นเท่านั้นซึ่งหมายความว่าประสิทธิภาพของอุปกรณ์นั้นดีขึ้น
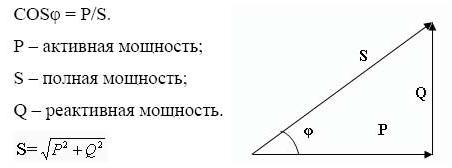
แนวคิดของพลังทั้งหมด สามเหลี่ยมพลัง
พลังงานปรากฏเป็นค่าที่คำนวณทางเรขาคณิตเท่ากับรากของผลรวมกำลังสองของกำลังเชิงโต้ตอบและกำลังสอง ตามลำดับ กำหนดด้วยอักษรละติน S.
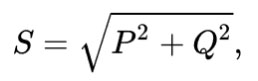
คุณยังสามารถคำนวณกำลังทั้งหมดโดยการคูณแรงดันและกระแสตามลำดับ
ส = U⋅I
สำคัญ! กำลังไฟฟ้าที่ปรากฎมีหน่วยวัดเป็นโวลต์แอมแปร์ (VA).
สามเหลี่ยมกำลังคือการแสดงที่สะดวกของการคำนวณและความสัมพันธ์ทั้งหมดที่อธิบายไว้ก่อนหน้านี้และความสัมพันธ์ระหว่างกำลังไฟฟ้าแบบแอ็คทีฟ รีแอกทีฟ และพลังงานปรากฏ
ขาสะท้อนส่วนประกอบที่ทำปฏิกิริยาและแอคทีฟ ด้านตรงข้ามมุมฉาก - กำลังทั้งหมด ตามกฎของเรขาคณิต โคไซน์ของมุม φ เท่ากับอัตราส่วนของส่วนประกอบที่ทำงานอยู่และส่วนประกอบทั้งหมด กล่าวคือ มันคือตัวประกอบกำลัง
วิธีค้นหาพลังงานที่แอคทีฟ ปฏิกิริยา และปรากฏ ตัวอย่างการคำนวณ
การคำนวณทั้งหมดขึ้นอยู่กับสูตรที่กล่าวถึงก่อนหน้านี้และรูปสามเหลี่ยมกำลัง ลองดูปัญหาที่พบบ่อยที่สุดในการปฏิบัติ
โดยปกติ เครื่องใช้ไฟฟ้าจะถูกทำเครื่องหมายด้วยกำลังไฟฟ้าที่ใช้งานและค่าของสัมประสิทธิ์cosφ ด้วยข้อมูลเหล่านี้ ทำให้ง่ายต่อการคำนวณส่วนประกอบปฏิกิริยาและส่วนประกอบทั้งหมด
ในการทำเช่นนี้ เราแบ่งกำลังงานด้วยค่าสัมประสิทธิ์ cosφ และรับผลคูณของกระแสและแรงดัน นี้จะเต็มไปด้วยพลัง
นอกจากนี้ จากรูปสามเหลี่ยมกำลัง เราพบกำลังไฟฟ้ารีแอกทีฟเท่ากับกำลังสองของผลต่างระหว่างกำลังสองของกำลังปรากฏและกำลังเชิงแอ็คทีฟ
วิธีวัด cosφ ในทางปฏิบัติ
ค่าของสัมประสิทธิ์cosφมักจะระบุไว้บนแท็กของเครื่องใช้ไฟฟ้าอย่างไรก็ตามหากจำเป็นต้องวัดในทางปฏิบัติพวกเขาจะใช้อุปกรณ์พิเศษ - เครื่องวัดเฟส. นอกจากนี้ wattmeter ดิจิตอลสามารถรับมือกับงานนี้ได้อย่างง่ายดาย

ถ้าค่าสัมประสิทธิ์ cosφ ที่ได้มานั้นต่ำพอ มันก็สามารถชดเชยได้ในทางปฏิบัติ ทำได้โดยการรวมอุปกรณ์เพิ่มเติมในวงจรเป็นหลัก
- หากจำเป็นต้องแก้ไขส่วนประกอบที่เกิดปฏิกิริยา ควรรวมองค์ประกอบที่ทำปฏิกิริยาไว้ในวงจร โดยทำหน้าที่ตรงข้ามกับอุปกรณ์ที่ทำงานอยู่แล้ว เพื่อชดเชยการทำงานของมอเตอร์เหนี่ยวนำ เช่น โหลดอุปนัย ตัวเก็บประจุเชื่อมต่อแบบขนาน มีการเชื่อมต่อแม่เหล็กไฟฟ้าเพื่อชดเชยมอเตอร์ซิงโครนัส
- หากจำเป็นต้องแก้ไขปัญหาที่ไม่เป็นเชิงเส้น ตัวแก้ไข cosφ แบบพาสซีฟจะถูกนำมาใช้ในวงจร ตัวอย่างเช่น อาจเป็นโช้กเหนี่ยวนำสูงที่เชื่อมต่อแบบอนุกรมกับโหลด
กำลังเป็นหนึ่งในตัวชี้วัดที่สำคัญที่สุดของเครื่องใช้ไฟฟ้า ดังนั้นการรู้ว่ามันคืออะไรและคำนวณอย่างไรจึงมีประโยชน์ไม่เพียงแต่สำหรับเด็กนักเรียนและผู้ที่เชี่ยวชาญด้านเทคโนโลยีเท่านั้น แต่ยังสำหรับเราแต่ละคนด้วย
บทความที่คล้ายกัน: