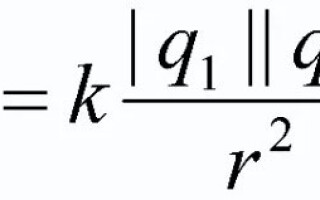ระหว่างวัตถุที่มีประจุมีแรงโต้ตอบเนื่องจากสามารถดึงดูดหรือผลักกัน กฎของคูลอมบ์อธิบายแรงนี้ แสดงระดับของการกระทำ ขึ้นอยู่กับขนาดและรูปร่างของตัวมันเอง กฎหมายทางกายภาพนี้จะกล่าวถึงในบทความนี้
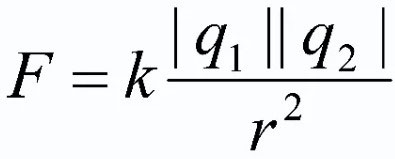
เนื้อหา
ค่าจุดเครื่องเขียน
กฎของคูลอมบ์ใช้กับวัตถุอยู่กับที่ซึ่งมีขนาดเล็กกว่าระยะห่างจากวัตถุอื่นมาก ประจุไฟฟ้าแบบจุดจะกระจุกตัวอยู่ที่วัตถุดังกล่าว เมื่อแก้ปัญหาทางกายภาพ มิติของร่างกายที่พิจารณาจะถูกละเลยเพราะ พวกเขาไม่สำคัญจริงๆ
ในทางปฏิบัติ การชาร์จแบบจุดที่เหลือจะแสดงดังนี้:


ในกรณีนี้ q1 และ q2 - นี่คือ เชิงบวก ประจุไฟฟ้าและแรงคูลอมบ์กระทำต่อประจุเหล่านี้ (ไม่แสดงในรูป) ขนาดของคุณสมบัติจุดไม่สำคัญ
บันทึก! ค่าใช้จ่ายที่เหลือจะอยู่ห่างจากกันซึ่งในปัญหามักเขียนแทนด้วยตัวอักษร r นอกจากนี้ในบทความ ค่าใช้จ่ายเหล่านี้จะได้รับการพิจารณาในสุญญากาศ
ความสมดุลของแรงบิดของ Charles Coulomb
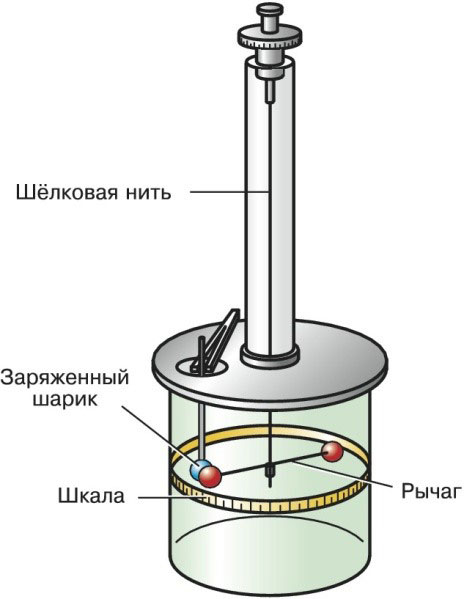
อุปกรณ์นี้พัฒนาโดยคูลอมบ์ในปี 1777 ช่วยในการสรุปการพึ่งพากองกำลังที่ตั้งชื่อตามเขาในภายหลัง ด้วยความช่วยเหลือของมันได้ทำการศึกษาปฏิสัมพันธ์ของประจุแบบจุดและขั้วแม่เหล็ก
เครื่องชั่งแบบบิดมีเส้นไหมขนาดเล็กอยู่ในระนาบแนวตั้งซึ่งมีคันโยกที่สมดุลห้อยอยู่ ค่าจุดจะอยู่ที่ปลายคันโยก
ภายใต้การกระทำของแรงภายนอก คันโยกเริ่มเคลื่อนที่ในแนวนอน คันโยกจะเคลื่อนที่ในระนาบจนกว่าจะสมดุลด้วยแรงยืดหยุ่นของเกลียว
ในกระบวนการเคลื่อนที่ คันโยกจะเบี่ยงเบนจากแกนตั้งเป็นมุมหนึ่ง มันถูกถ่ายเป็น d และเรียกว่ามุมของการหมุน เมื่อทราบค่าของพารามิเตอร์นี้แล้ว ก็สามารถหาแรงบิดของแรงที่เกิดขึ้นได้
ความสมดุลของแรงบิดของ Charles Coulomb มีลักษณะดังนี้:
ปัจจัยสัดส่วน k และค่าคงที่ทางไฟฟ้า 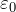
ในสูตรของกฎของคูลอมบ์มีพารามิเตอร์ k - สัมประสิทธิ์สัดส่วนหรือ ![]() คือค่าคงที่ทางไฟฟ้า ค่าคงที่ทางไฟฟ้า
คือค่าคงที่ทางไฟฟ้า ค่าคงที่ทางไฟฟ้า ![]() นำเสนอในหนังสืออ้างอิง ตำราเรียน อินเทอร์เน็ตมากมาย ไม่ต้องนับ! ปัจจัยสัดส่วนสูญญากาศขึ้นอยู่กับ
นำเสนอในหนังสืออ้างอิง ตำราเรียน อินเทอร์เน็ตมากมาย ไม่ต้องนับ! ปัจจัยสัดส่วนสูญญากาศขึ้นอยู่กับ ![]() สามารถพบได้โดยสูตรที่รู้จักกันดี:
สามารถพบได้โดยสูตรที่รู้จักกันดี:
![]()
ที่นี่ ![]() คือค่าคงที่ทางไฟฟ้า
คือค่าคงที่ทางไฟฟ้า
![]() - ปี่
- ปี่
![]() คือสัมประสิทธิ์สัดส่วนในสุญญากาศ
คือสัมประสิทธิ์สัดส่วนในสุญญากาศ
ข้อมูลเพิ่มเติม! หากไม่ทราบพารามิเตอร์ที่แสดงข้างต้น จะไม่สามารถค้นหาแรงปฏิสัมพันธ์ระหว่างประจุไฟฟ้าสองจุดได้
สูตรและสูตรของกฎของคูลอมบ์
เพื่อสรุปข้างต้น จำเป็นต้องกำหนดกฎหลักของไฟฟ้าสถิตอย่างเป็นทางการ มันใช้แบบฟอร์ม:
แรงปฏิสัมพันธ์ของประจุสองจุดที่หยุดนิ่งในสุญญากาศนั้นแปรผันโดยตรงกับผลคูณของประจุเหล่านี้ และเป็นสัดส่วนผกผันกับกำลังสองของระยะห่างระหว่างพวกมัน ยิ่งกว่านั้นผลิตภัณฑ์ของค่าใช้จ่ายจะต้องใช้โมดูโล่!
![]()
ในสูตรนี้ q1 และ q2 เป็นค่าใช้จ่ายจุด ถือเป็นร่างกาย; r2 - ระยะทางบนระนาบระหว่างวัตถุเหล่านี้ ถ่ายในสี่เหลี่ยมจัตุรัส k คือสัมประสิทธิ์ของสัดส่วน (![]() สำหรับสุญญากาศ)
สำหรับสุญญากาศ)
ทิศทางของแรงคูลอมบ์และรูปเวกเตอร์ของสูตร
เพื่อให้เข้าใจสูตรอย่างสมบูรณ์ กฎของคูลอมบ์สามารถแสดงเป็นภาพได้:
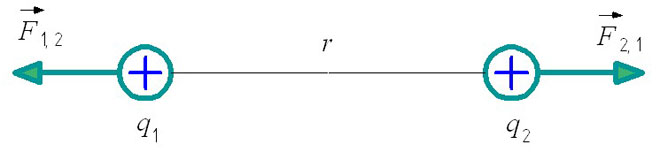
F1,2 - แรงโต้ตอบของประจุแรกเทียบกับประจุที่สอง
F2,1 - แรงโต้ตอบของประจุที่สองที่สัมพันธ์กับประจุแรก
นอกจากนี้ เมื่อแก้ปัญหาไฟฟ้าสถิต จำเป็นต้องคำนึงถึงกฎสำคัญ: การขับไล่ประจุไฟฟ้าที่มีชื่อเดียวกัน และการดึงดูดประจุตรงข้าม ตำแหน่งของแรงปฏิสัมพันธ์ในรูปขึ้นอยู่กับสิ่งนี้
หากพิจารณาประจุที่ตรงกันข้าม พลังของการมีปฏิสัมพันธ์จะพุ่งเข้าหากันโดยแสดงถึงแรงดึงดูด
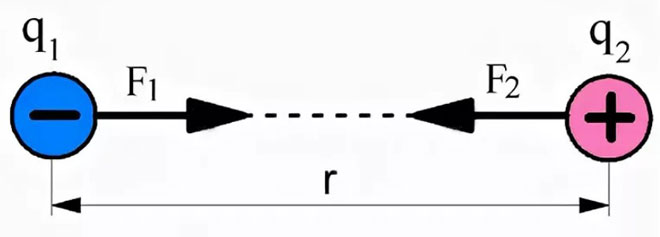
สูตรของกฎพื้นฐานของไฟฟ้าสถิตในรูปแบบเวกเตอร์สามารถแสดงได้ดังนี้:
![]()
![]() คือแรงที่กระทำต่อจุดประจุ q1 จากด้านข้างของประจุ q2
คือแรงที่กระทำต่อจุดประจุ q1 จากด้านข้างของประจุ q2
![]() คือเวกเตอร์รัศมีเชื่อมต่อประจุ q2 กับประจุ q1
คือเวกเตอร์รัศมีเชื่อมต่อประจุ q2 กับประจุ q1
![]()
สำคัญ! เมื่อเขียนสูตรในรูปแบบเวกเตอร์แล้ว แรงโต้ตอบของประจุไฟฟ้าสองจุดจะต้องถูกฉายลงบนแกนเพื่อให้เครื่องหมายถูกต้อง การกระทำนี้เป็นพิธีการและมักจะกระทำโดยปราศจากการจดบันทึกใดๆ
ในกรณีที่ใช้กฎของคูลอมบ์ในทางปฏิบัติ
กฎพื้นฐานของไฟฟ้าสถิตคือการค้นพบที่สำคัญที่สุดของ Charles Coulomb ซึ่งพบว่ามีการนำไปใช้ในหลายพื้นที่
ผลงานของนักฟิสิกส์ที่มีชื่อเสียงถูกนำมาใช้ในกระบวนการประดิษฐ์อุปกรณ์เครื่องมือต่างๆ ตัวอย่างเช่นสายล่อฟ้า
ด้วยความช่วยเหลือของสายล่อฟ้า อาคารที่พักอาศัยและอาคารต่างๆ ได้รับการปกป้องจากฟ้าผ่าระหว่างพายุฝนฟ้าคะนอง ดังนั้นระดับการป้องกันอุปกรณ์ไฟฟ้าจึงเพิ่มขึ้น
สายล่อฟ้าทำงานตามหลักการต่อไปนี้: ระหว่างพายุฝนฟ้าคะนอง ประจุเหนี่ยวนำอย่างแรงจะค่อยๆ เริ่มสะสมบนพื้นดิน ซึ่งจะลอยขึ้นและดึงดูดไปยังก้อนเมฆ ในกรณีนี้สนามไฟฟ้าค่อนข้างใหญ่จะเกิดขึ้นบนพื้นดิน ใกล้สายล่อฟ้า สนามไฟฟ้าจะแข็งแกร่งขึ้น เนื่องจากประจุไฟฟ้าโคโรนาถูกจุดไฟจากส่วนปลายของอุปกรณ์
นอกจากนี้ ประจุที่เกิดขึ้นบนพื้นเริ่มดึงดูดประจุของเมฆด้วยเครื่องหมายตรงข้าม ตามที่ควรเป็นไปตามกฎของชาร์ลส์ คูลอมบ์ หลังจากนั้น อากาศจะผ่านกระบวนการไอออไนเซชัน และความแรงของสนามไฟฟ้าจะลดลงเมื่ออยู่ใกล้ปลายสายล่อฟ้า ดังนั้นความเสี่ยงที่ฟ้าผ่าจะเข้ามาในอาคารจึงน้อยมาก
บันทึก! หากอาคารที่ติดตั้งสายล่อฟ้าถูกติดตั้งจะไม่มีไฟและพลังงานทั้งหมดจะลงไปที่พื้น
ตามกฎของคูลอมบ์ อุปกรณ์ที่เรียกว่า "ตัวเร่งอนุภาค" ได้รับการพัฒนาซึ่งเป็นที่ต้องการอย่างมากในปัจจุบัน
ในอุปกรณ์นี้มีการสร้างสนามไฟฟ้าแรงสูงซึ่งจะเพิ่มพลังงานของอนุภาคที่ตกลงมา
ทิศทางของแรงในกฎของคูลอมบ์
ดังที่ได้กล่าวไว้ข้างต้น ทิศทางของแรงโต้ตอบของประจุไฟฟ้าสองจุดขึ้นอยู่กับขั้วของพวกมัน เหล่านั้น. การเรียกเก็บเงินที่มีชื่อเดียวกันจะถูกยกเลิกและการเรียกเก็บเงินจากการเรียกเก็บเงินที่ตรงกันข้ามจะดึงดูด
แรงคูลอมบ์สามารถเรียกได้ว่าเวกเตอร์รัศมีเพราะ พวกมันถูกกำกับไปตามเส้นที่ลากระหว่างพวกเขา
ในปัญหาทางกายภาพบางอย่างจะมีการให้ร่างกายที่มีรูปร่างซับซ้อนซึ่งไม่สามารถนำมาเป็นประจุไฟฟ้าได้เช่น ละเลยขนาดของมัน ในสถานการณ์นี้ ร่างกายที่กำลังพิจารณาจะต้องแบ่งออกเป็นส่วนเล็กๆ หลายๆ ส่วน และแต่ละส่วนจะต้องคำนวณแยกกัน โดยใช้กฎของคูลอมบ์
เวกเตอร์แรงที่ได้จากการแยกจะถูกสรุปตามกฎของพีชคณิตและเรขาคณิต ผลที่ได้คือแรงที่เกิดขึ้นซึ่งจะเป็นคำตอบสำหรับปัญหานี้ วิธีการแก้นี้มักจะเรียกว่าวิธีสามเหลี่ยม
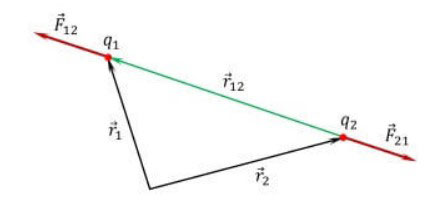
ประวัติความเป็นมาของการค้นพบกฎหมาย
การโต้ตอบของการเรียกเก็บเงินสองจุดตามกฎหมายที่พิจารณาข้างต้นได้รับการพิสูจน์ครั้งแรกในปี พ.ศ. 2328 โดย Charles Coulomb นักฟิสิกส์พยายามพิสูจน์ความจริงของกฎหมายที่จัดทำขึ้นโดยใช้เครื่องชั่งแบบทอร์ชันซึ่งเป็นหลักการของการทำงานซึ่งถูกนำเสนอในบทความด้วย
คูลอมบ์ยังพิสูจน์ด้วยว่าไม่มีประจุไฟฟ้าในตัวเก็บประจุแบบทรงกลม ดังนั้นเขาจึงมาถึงคำแถลงว่าขนาดของแรงไฟฟ้าสถิตสามารถเปลี่ยนแปลงได้โดยการเปลี่ยนระยะห่างระหว่างวัตถุที่อยู่ระหว่างการพิจารณา
ดังนั้น กฎของคูลอมบ์จึงเป็นกฎที่สำคัญที่สุดของไฟฟ้าสถิต บนพื้นฐานของการค้นพบที่ยิ่งใหญ่ที่สุดมากมาย ภายในกรอบของบทความนี้ มีการนำเสนอถ้อยคำที่เป็นทางการของกฎหมาย ตลอดจนอธิบายส่วนประกอบต่างๆ อย่างละเอียด
บทความที่คล้ายกัน: